Question

Find the Hamilton-Jacobi equation (with terminal values) corresponding to the optimal control problem of minimizing: J[x(⋅)] =∫ᵗ₀[ 1/4(x(t))⁴ + x(t)] dt You can proceed to find the Hamilton-Jacobi equation associated with this optimal control problem, including any terminal values if necessary.

Answer 1

The Hamilton-Jacobi equation corresponding to the optimal control problem of minimizing
`\( J[x(\cdot)] = \int_(t_0)^(t) \left((1)/(4)(x(t))^4 + x(t)\right) dt \)` is given by
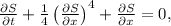`\( (\partial S)/(\partial t) + (1)/(4)\left((\partial S)/(\partial x)\right)^4 + (\partial S)/(\partial x) = 0 \),`with the terminal condition
`\( S(T, x(T)) = 0 \).`

Step-by-step explanation:

In the optimal control problem, the objective is to minimize the functional
`\( J[x(\cdot)] = \int_(t_0)^(T) \left((1)/(4)(x(t))^4 + x(t)\right) dt \),` where
`\( x(t) \)` is the state trajectory. The Hamilton-Jacobi equation for this problem is derived by considering the Hamiltonian function
`\( H = (1)/(4)p^4 + p \),`where
`\( p \)`is the conjugate momentum.

The Hamilton-Jacobi equation is given by
`\( (\partial S)/(\partial t) + H\left(t, x, (\partial S)/(\partial x)\right) = 0 \), where \( S \)`is the Hamiltonian characteristic function. Substituting the expression for
`\( H \),` we get
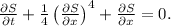`\( (\partial S)/(\partial t) + (1)/(4)\left((\partial S)/(\partial x)\right)^4 + (\partial S)/(\partial x) = 0 \).` This is the Hamilton-Jacobi equation associated with the given optimal control problem.

The terminal condition
`\( S(T, x(T)) = 0 \)` is included to account for the final time constraint. It ensures that the solution satisfies the given boundary condition at the final time
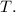`\( T \).`This terminal condition is essential for obtaining a unique solution to the Hamilton-Jacobi equation in the context of optimal control problems.