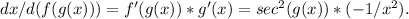Final answer:
To find the derivative of the function
 the chain rule. We differentiate the outer function, tan(x), and the inner function,
the chain rule. We differentiate the outer function, tan(x), and the inner function,
 separately, and then multiply the results.
separately, and then multiply the results.
Step-by-step explanation:
To find the derivative of the function y = tan (1/x), we can use the chain rule. Let's start by defining
 The Chain Rule states that the derivative of f(g(x)) is equal to
The Chain Rule states that the derivative of f(g(x)) is equal to
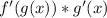
To find f'(g(x)), we differentiate f(x) with respect to x and evaluate it at g(x). The derivative of tan(x) is
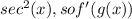
To find g'(x), we differentiate g(x) with respect to x. Using the power rule, we get
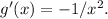
Now, we can apply the chain rule: