Final Answer:
A) The sequence of functions
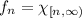 is decreasing and converges uniformly to a limit function f. However,
is decreasing and converges uniformly to a limit function f. However,
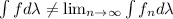 , illustrating that the Monotone Convergence Theorem does not hold for decreasing functions.
, illustrating that the Monotone Convergence Theorem does not hold for decreasing functions.
Step-by-step explanation:
In this example, each function
 is defined as the characteristic function of the set
is defined as the characteristic function of the set
 , denoted by
, denoted by
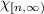 . Firstly, we establish that
. Firstly, we establish that
 is decreasing. As n increases, the set
is decreasing. As n increases, the set
 becomes larger, causing
becomes larger, causing
 to take the value 1 on a smaller set, hence decreasing.
to take the value 1 on a smaller set, hence decreasing.
Secondly, to show uniform convergence, for any
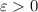 , we can choose N such that for all
, we can choose N such that for all
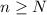 ,
,
 , where f is the pointwise limit of
, where f is the pointwise limit of
 . This implies that
. This implies that
 converges uniformly to f.
converges uniformly to f.
Finally, the failure of the Monotone Convergence Theorem is evident when evaluating the integrals. The integral of the limit function f is not equal to the limit of the integrals of
 . This discrepancy arises due to the unbounded nature of the sets
. This discrepancy arises due to the unbounded nature of the sets
 , leading to a failure in the conditions required for the Monotone Convergence Theorem.
, leading to a failure in the conditions required for the Monotone Convergence Theorem.