Question

Convert the second-order differential equation

d²y/d²t+2y=0 into a first-order system in terms of y and v, where v=dy/dt.
(a) Determine the vector field associated with the first-order system.
(b) Sketch enough vectors in the vector field to get a sense of its geometric structure. (You should do this part of the exercise without the use of technology.)
(c) Use HPGSystemsolver to sketch the associated direction field.
(d) Make a rough sketch of the phase portrait of the system and confirm your answer using HPGSystemsolver.
(e) Briefly describe the behavior of the solutions.

Answer 1

To convert the second-order differential equation d²y/d²t+2y=0 into a first-order system in terms of y and v, we can substitute v=dy/dt into the equation. The vector field associated with the first-order system can be represented by (dv/dt, -2y). Sketching enough vectors in the vector field can provide a sense of its geometric structure. HPGSystemsolver can be used to sketch the associated direction field and make a rough phase portrait of the system.

Step-by-step explanation:

To convert the second-order differential equation d²y/d²t+2y=0 into a first-order system, we can define a new variable v = dy/dt. Substituting this into the equation, we get:

`dv/dt + 2y = 0`

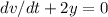
This gives us a first-order system with two variables: y and v.

(a) The vector field associated with the first-order system can be represented by the vector (dv/dt, -2y).

(b) Sketching enough vectors in the vector field can provide a sense of its geometric structure. Without the use of technology, you can draw arrows representing the vectors at various points in the y-v plane based on different values of y and v.

(c) HPGSystemsolver can be used to sketch the associated direction field, which can show the slope of the vector at each point in the y-v plane.

(d) Using the direction field, you can make a rough sketch of the phase portrait of the system, which shows the behavior of the solutions. HPGSystemsolver can also be used to confirm the accuracy of your sketch.

(e) The behavior of the solutions can vary depending on the initial conditions. The phase portrait and direction field can provide insights into the stability, limit cycles, and other patterns that may be present in the system.