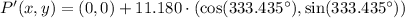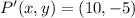Answer:
There are two possible solutions:
Clockwise rotation
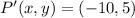
Counterclockwise rotation
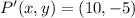
Explanation:
There are two possible answers: (i) Clockwise rotation, (ii) Counterclockwise rotation. Vectorially speaking, rotation of point of rotation of a point about another point of reference is defined by:
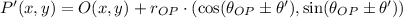 (1)
(1)
Where:
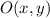 - Point of reference.
- Point of reference.
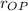 - Length of the segment OP.
- Length of the segment OP.
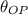 - Direction of segment OP, measured in sexagesimal degrees.
- Direction of segment OP, measured in sexagesimal degrees.
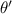 - Angle of rotation, measured in sexagesimal degrees.
- Angle of rotation, measured in sexagesimal degrees.
Please notice that clockiwise rotation occurs when
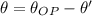 and counterclockwise rotation when
and counterclockwise rotation when
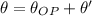 . In addition, we define length and direction of the segment below:
. In addition, we define length and direction of the segment below:
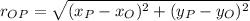 (1)
(1)
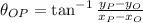
If we know that
 ,
,
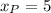 ,
,
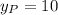 and
and
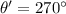 , then the coordinates of the first car after rotation is:
, then the coordinates of the first car after rotation is:
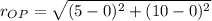
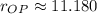
Please notice that original point is located at first quadrant of the Cartesian plane centered at origin, then the direction of the segment OP is:
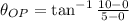

The two solutions are finally presented:
Clockwise rotation
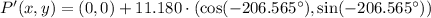
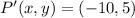
Counterclockwise rotation