Question

What are the coordinates of the hole in the function?

f(x)=2x^2−5x−12 / 3x^2−11x−4
Enter your answer by filling in the boxes. Enter your answer as simplified fractions, as necessary.

Answer 1

The coordinates of the hole in the function f(x) are (4, 11/13), which is found by factoring the numerator and denominator, identifying the common factor, and evaluating the simplified function at the value of x that corresponds to the common factor.

Step-by-step explanation:

The question asks for the coordinates of the hole in the function
`f(x) = (2x^2 - 5x - 12)/(3x^2 - 11x - 4)`. To find the hole, we need to factor both the numerator and the denominator to look for any common factors that would result in an undefined point in the function where the hole would occur.

First, let's factor the numerator and denominator:

Numerator: 2x^2 - 5x - 12 can be factored into (2x + 3)(x - 4).

Denominator: 3x^2 - 11x - 4 can be factored into (3x + 1)(x - 4).

Now, we can see that the term (x - 4) is common to both the numerator and the denominator, indicating a hole in the graph of the function when x = 4.

To find the y-coordinate of the hole, we substitute x = 4 into the simplified function after removing the common factor:

`f(x) = (2x + 3)/(3x + 1)`

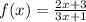
Substituting x = 4 gives us:

`f(4) = (2(4) + 3)/(3(4) + 1) = (11)/(13)`

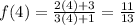
Thus, the coordinates of the hole are (4, 11/13).