Question

Scarlett is 1.85 meters tall. At 1 p.m., she measures the length of a tree's shadow to be 33.75 meters. She stands 28.6 meters away from the tree, so that the tip of her shadow meets the tip of the tree's shadow. Find the height of the tree to the nearest hundredth of a meter.

Answer 1

The height of the tree is approximately 1.56 meters.

To find the height of the tree, we can set up a proportion using the similar triangles formed by Scarlett and the tree.

Let H be the height of the tree.

The proportion can be set up as follows:

`(Height of Scarlett)/(length of Scarlett shadow) =(Height of Tree)/(length of trees shadow)`

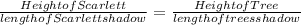
Substitute the given values:

`(1.85m)/(33.75m) =(H)/(28.6m)`

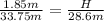
Now, solve for H:

`H= (1.85m * 28.6m)/(33.75m)`

Calculate this value:

`H= (52.71)/(33.75)= 1.56m`

So, the height of the tree is approximately 1.56 meters.