 and
and
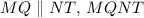 is a parallelogram, and thus
is a parallelogram, and thus
 by the properties of a parallelogram.
by the properties of a parallelogram.
The image contains a geometric diagram with a quadrilateral
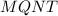 and a line segment
and a line segment
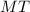 . The following information is given and required to be proved:
. The following information is given and required to be proved:
Given:


Prove:

The diagram shows quadrilateral
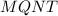 with
with
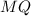 and
and
 as opposite sides and
as opposite sides and
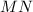 and
and
 as the other pair of opposite sides. There are arrows on lines
as the other pair of opposite sides. There are arrows on lines
 indicating they are parallel, and tick marks on
indicating they are parallel, and tick marks on
 indicating they are of equal length.
indicating they are of equal length.
To solve the given problem, we will use properties of parallelograms, as the given information suggests that
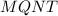 could be a parallelogram.
could be a parallelogram.
Given:

To Prove:

Step 1: Identify Properties
If one pair of opposite sides of a quadrilateral are both congruent and parallel, then the quadrilateral is a parallelogram.
Step 2: Apply Properties
- By the definition of a parallelogram, the opposite sides are congruent. Therefore, if
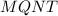 is a parallelogram, then
is a parallelogram, then
 .
.
Step 3: Conclusion
Since
 and
and
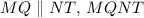 is a parallelogram, and thus
is a parallelogram, and thus
 by the properties of a parallelogram.
by the properties of a parallelogram.