Question

-6x - y = 10 12x + 2y = -20 system of equations by elimination with multiplication

Answer 1

The system has infinitely many solutions as the equations represent the same line, making them dependent.

Sure, to solve this system of equations using the elimination method with multiplication, we'll aim to eliminate one of the variables by making the coefficients of either \(x\) or \(y\) the same in both equations. Let's start with your equations:

`Equation 1: \(-6x - y = 10\)`

`Equation 2: \(12x + 2y = -20\)`

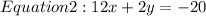
To eliminate
`\(y\),` we can manipulate these equations by multiplying both sides of Equation 1 by 2 to match the coefficient of
`\(y\)` in Equation 2:

Multiply Equation 1 by 2:

`\(2(-6x - y = 10)\)`

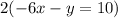
This becomes:
`\(-12x - 2y = 20\)`

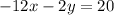
Now, let's align this with Equation 2:

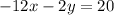`\(-12x - 2y = 20\)` (Equation 1 after multiplication)

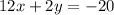`\(12x + 2y = -20\)`(Equation 2)

By adding these two equations together, we can eliminate \(y\):

`\((-12x - 2y) + (12x + 2y) = 20 - 20\)`

`\(-12x + 12x - 2y + 2y = 0\)`

`\(0 = 0\)`

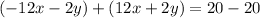
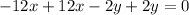
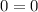
This equation shows that x cancels out, resulting in an identity that implies the two equations are representing the same line. This means they are dependent equations, and the solution is infinitely many points that satisfy both equations.

In conclusion, the given system of equations has infinitely many solutions since the equations represent the same line. This occurs because the coefficients of x and y are in a constant ratio, making the system dependent rather than having a unique solution.