Question

Write the complex number in trigonometric form

A) $r(\cos \theta + i \sin \theta)$
B) $r(\cos \theta - i \sin \theta)$
C) $r(\cos \theta + \sin \theta)$
D) $r(\cos \theta - \sin \theta)$

Answer 1

The complex number in trigonometric form is A)
`$r(\cos \theta + i \sin \theta)$`.

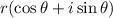Explaination:

To represent a complex number in trigonometric form, we utilize Euler's formula:
`$z = r(\cos \theta + i \sin \theta)$`, where
`$z$` is the complex number,
`$r$` is the magnitude, and
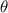`$\theta$` is the angle.

In this case, the form A)
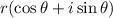`$r(\cos \theta + i \sin \theta)$` corresponds to the standard form of a complex number in trigonometric notation. The expression
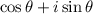`$\cos \theta + i \sin \theta$` is derived from Euler's formula, which relates complex numbers to trigonometric functions. Here,
`$\cos \theta$` represents the real part of the complex number, and
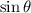`$\sin \theta$` represents the imaginary part, combined with the angle
`$\theta$`.

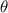The use of
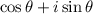`$\cos \theta + i \sin \theta$` represents the magnitude
`$r$` along with the angle
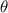`$\theta$` in the complex plane. It is a concise and standard way of expressing complex numbers, highlighting both magnitude and direction in terms of trigonometric functions, making it a convenient form for various mathematical operations and analyses involving complex numbers.