Final Answer:
The critical points are found by setting the derivative of
 equal to zero, and evaluating the second derivative confirms that
equal to zero, and evaluating the second derivative confirms that
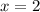 corresponds to a local minimum. The correct option is B).
corresponds to a local minimum. The correct option is B).
Step-by-step explanation:
The critical points of a function occur where its derivative is zero or undefined. To find the critical points of
 , we need to find its derivative
, we need to find its derivative
 . Let's calculate that:
. Let's calculate that:
![\[f'(x) = 2x - 18x²\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/9hel26r4gtx88gn9m6q77jx40ysn3yzkdd.png)
Setting
 equal to zero gives us the critical points:
equal to zero gives us the critical points:
![\[2x - 18x² = 0\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/60lv8sg0b666xh0v5hevk8jhk32xmzlq4h.png)
Factoring out
 , we get:
, we get:
![\[2x(1 - 9x) = 0\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/u2pvnjv5w8wjenqjht8qaa9wyocr1jgt06.png)
So, the critical points are
 and
and
 . Now, we evaluate the second derivative,
. Now, we evaluate the second derivative,
 , to determine the nature of these critical points. The second derivative is:
, to determine the nature of these critical points. The second derivative is:
![\[f''(x) = 2 - 36x\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/a1w2kh5m5hano2qvhwy6u01rps5kzcv5h3.png)
Evaluating
 gives a positive value, indicating a local minimum, while
gives a positive value, indicating a local minimum, while
 is negative, indicating a local maximum. Therefore, the function has a minimum at
is negative, indicating a local maximum. Therefore, the function has a minimum at
 and a maximum at
and a maximum at
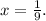
However,
 is not within the given options, so we consider the next critical point. Evaluating
is not within the given options, so we consider the next critical point. Evaluating
 gives a positive value, confirming a local minimum at
gives a positive value, confirming a local minimum at
 Thus, the final answer is that the function
Thus, the final answer is that the function
 has a minimum value at
has a minimum value at
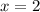 . Therefore option B is correct.
. Therefore option B is correct.