Question

At the Local Order-place of Pancakes (LOOP), all you can do is

order pancakes in stacks of three. In fact, you must specify
which pancake is on top, which is in the middle, and which is on the bottom. The waitstaff
refer to this as "stack order." There are six pancake flavors (blueberry, chocolate chip, apple
cinnamon, pecan, buttermilk, banana).
a. How many possible pancake orders are there (specifying flavor and stack order)?
b. How many different pancake orders involve three different flavors of pancakes?
hin and one

Answer 1

The total number of possible pancake orders is 216. There are 20 different pancake orders involving three different flavors.

a. To determine the total number of possible pancake orders, considering the flavor and stack order, you can use the multiplication principle.

For each stack order (top, middle, bottom), there are 6 choices of flavors. Therefore, the total number of possible pancake orders is:

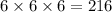`\(6 * 6 * 6 = 216\)` orders.

b. To find the number of different pancake orders involving three different flavors, you need to choose three distinct flavors out of the six available. This is a combination problem.

The number of ways to choose three different flavors out of six is denoted as
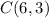`\(C(6, 3)\)` and is calculated as:

`\[ C(6, 3) = (6!)/(3!(6-3)!) = (6 * 5 * 4)/(3 * 2 * 1) = 20 \]`

So, there are 20 different pancake orders involving three different flavors.