Question

What is the minimum energy required to launch a satellite of mass m from the surface of a planet of mass M and radius R in a circular orbit at an altitude of 2R?

Answer 1

The minimum energy required is
`\((3)/(2)GM \cdot R\)`.

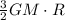How to determine minimum energy?

To calculate the minimum energy required to launch a satellite from the surface of a planet to a circular orbit at an altitude of 2R, use the gravitational potential energy and kinetic energy.

The gravitational potential energy (U) is given by:

`\[ U = -(GMm)/(r) \]`

where:

G = gravitational constant (
`\(6.67 * 10^(-11) \, \text{Nm}^2/\text{kg}^2\)`),

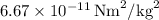M = mass of the planet,

m = mass of the satellite,

r = distance from the center of the planet to the satellite.

The kinetic energy (K) is given by:

`\[ K = (1)/(2)mv^2 \]`

where:

v = velocity of the satellite in the circular orbit.

For a circular orbit, the velocity (v) is related to the gravitational parameter (GM) and the radius of the orbit (r) by:

`\[ v = \sqrt{(GM)/(r)} \]`

Now, set the kinetic energy equal to the absolute value of the gravitational potential energy:

`\[ (1)/(2)mv^2 = (GMm)/(r) \]`

Substitute
`\(v = \sqrt{(GM)/(r)}\)` into the equation:

`\[ (1)/(2)m\left(\sqrt{(GM)/(r)}\right)^2 = (GMm)/(r) \]`

Simplify the equation:

`\[ (1)/(2)GMm = (GMm)/(r) \]`

Multiply both sides by r:

`\[ (1)/(2)GMm \cdot r = GMm \]`

Now, find the minimum energy when the satellite is at an altitude of 2R, so r = 3R (radius of the planet plus altitude):

`\[ (1)/(2)GMm \cdot 3R = GMm \]`

Simplify:

`\[ (3)/(2)GM \cdot R \]`

So, the minimum energy required is
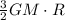`\((3)/(2)GM \cdot R\)`.