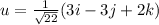Question

If →a=i+j+k,→b=2i−j+3k and →c=i−2j+k, find a unit vector parallel to the vector 2→a−→b+3→c .

Answer 1

The unit vector parallel to the vector 2a - b + 3c is determined as
`(1)/(√(22) ) (3i - 3j + 2k)`.

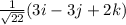How to calculate the parallel vector?

The unit vector parallel to the vector 2a - b + 3c is calculated as follows.

The given vectors;

a = i + j + k

b = 2i - j + 3k

c = i - 2j + k

The given vector 2a - b + 3c is calculated as follows;

v = 2(i + j + k) - (2i - j + 3k) + 3(i - 2j + k)

v = 2i + 2j + 2k - 2i + j - 3k + 3i - 6j + 3k

v = 3i -3j + 2k

The unit vector parallel to the above vector (v) is calculated as;

u = (v) / ||v||

The determinant of the vector is calculated by applying the following formula.

||v|| = √[(3² + (-3)² + (2²)]

||v|| = √22

`u = (1)/(√(22) ) (3i - 3j + 2k)`