Question

If acceleration due to gravity on Earth's surface is g, then find acceleration due to gravity on the surface of another planet whose radius is twice the radius of Earth and whose density is half:

a) 2g
b) g
c) 0.5g
d) 0.25g

Answer 1

The acceleration due to gravity on the surface of the other planet is 4 times that of Earth, which is 0.25g.

How to find acceleration due to gravity?

Mass (M) = proportional to density (ρ) and volume (V):

M = ρ × V

Density (ρ) = half that of Earth.

Volume (V) = proportional to R³, and R is doubled:

V = (2R)³

= 8R³

Therefore, the mass of the other planet is 8 × (0.5) = 4 times that of Earth.

The radius (R) is doubled.

Plugging these values into the formula for g:

`g_(other)_(planet) = G * 4M_(Earth) / (2R_(Earth)\pi )^2`

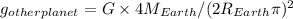
g' = g × (0.5M / M) × (R / (2R))²

= g × 0.5 × (1/4)

= 0.25g

Since G and
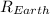`R_{Earth` cancel out, left with:

`g_(other)_(planet) = 4 * g_{Earth`

Therefore, the acceleration due to gravity on the surface of the other planet is 4 times that of Earth, which is 0.25g.

So, the answer is d) 0.25g.