Question

Verify that the function satisfies Rolle's Theorem for the square root.

a) Yes, it satisfies Rolle's Theorem
b) No, it does not satisfy Rolle's Theorem
c) Insufficient information
d) Rolle's Theorem is not applicable

Answer 1

To verify if Rolle's Theorem applies to a square root function, we need to ensure the function is continuous and differentiable on a certain interval and has equal values at endpoints. Without specific information about the function and interval, we cannot confirm Rolle's Theorem's applicability so the answer is 'Insufficient information.'

Step-by-step explanation:

To verify that the function satisfies Rolle's Theorem for the square root, we need to consider the criteria for Rolle's Theorem which are:

• The function must be continuous on the closed interval
  `[a, b]`.
• The function must be differentiable on the open interval
  `(a, b)`.
• The function must have equal values at the endpoints of the interval, which means
  `f(a) = f(b)`.

Given that the function in question involves a square root, we must ensure that the square root function satisfies all these conditions for some interval
`[a, b]`.

If, for example the function is
`f(x) = √x`, and the interval is
`[0, 4]`, we know that:

• 
  `f(x)` is continuous on
  `[0, 4]`.
• 
  `f(x)` is differentiable on
  `(0, 4)` but not at
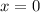  `x=0` because the derivative of
  `√x is (1/(2√x))`, which is undefined at
  `x = 0`.
• 
  `f(0) = √0 = 0` and
  `f(4) = √4 = 2`, which shows that
  `f(a) ≠ f(b)`.

Therefore, without more specific information about the function and the interval, we cannot confirm whether Rolle's Theorem applies. As such, the correct answer is c) Insufficient information.