Question

Using path integration from point (-1,3) to point (1,5), show that 9x²y²,dx + 6x³y,dy is an exact differential.

Answer 1

The expression (9x²y² ,dx + 6x³y ,dy) is an exact differential.

Step-by-step explanation:

To determine if the given expression is an exact differential, we need to check if the mixed partial derivatives with respect to (x) and (y) are equal. The expression is an exact differential if and only if:

`\[ (\partial)/(\partial y)(9x^2y^2) = (\partial)/(\partial x)(6x^3y) \]`

Let's calculate the partial derivatives:

1.
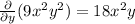
`\((\partial)/(\partial y)(9x^2y^2) = 18x^2y\)`

2.
`\((\partial)/(\partial x)(6x^3y) = 18x^2y\)`

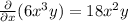
Since
`\((\partial)/(\partial y)(9x^2y^2) = (\partial)/(\partial x)(6x^3y)\)`, the expression is an exact differential.

Now, we can find the potential function \(U(x, y)\) by integrating the given expression with respect to \(x\) and then integrating the result with respect to \(y\):

`\[ U(x, y) = \int (9x^2y^2 \,dx + 6x^3y \,dy) \]`

Integrating the first term with respect to (x) gives (3x³y² + C(y)), where (C(y)) is a constant of integration. Now, integrating the result with respect to (y) gives:

`\[ U(x, y) = x^3y^3 + C(y) \]`

Thus, the potential function
`\(U(x, y) = x^3y^3 + C(y)\)` confirms that
`\(9x^2y^2 \,dx + 6x^3y \,dy\)` is indeed an exact differential.