Question

1100-kg car is slowly picking up speed as it goes around a horizontal unbanked curve whose radius is 180 m.

The coefficient of static friction between the tires and the road is 0.95.

At what speed will the car begin to skid sideways?

Answer 1

Here to keep the car on the track and prevent in from skiding, frictional force is required. Since the car is moving on a curve this frictional force is provided in the form of centripetal force.

Centripetal force is given as,

`\longrightarrow \rm Centripetal \ Force =(m v^2)/(r)`

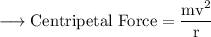
Since the curve is unbanked, frictional force is given as,

`\longrightarrow \rm Frictional \ force\ = \mu mg`

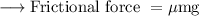
where ,

• m is the mass of the car.
• v is the velocity of the car.
• r is the radius of the curve.
• μ is the coefficient of static friction.
• g is acceleration due to gravity.

So we have;

`\longrightarrow (mv^2)/(r)=\mu mg \\\\`

`\longrightarrow (v^2)/(r)= \mu g \\\\`

`\longrightarrow v^2 = \mu rg \\\\`

`\longrightarrow v =√(\mu rg) \\\\`

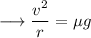
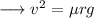
This velocity is the maximum velocity beyond which the car will begin to skid. On substituting the respective values, we have;

`\longrightarrow v = √(0.95 * 180m * 9.8\ m/s^2) \\\\`

`\longrightarrow v =√(1675.8) m/s \\\\`

`\longrightarrow \underline{\underline{v \approx 40.93 \ m/s }}\\\\`

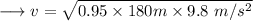
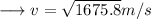
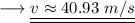
Hence the car begins to skid approximately at a velocity of 41m/s.