Question

The following reaction is a first-order reaction. If the

concentration is .256M after 145 seconds with k being .039/second,
what was the initial concentration? What is the half-life?

Answer 1

The initial concentration of the reaction was approximately 73.21 M. The half-life of the reaction is approximately 17.72 seconds.

The initial concentration of the reaction can be determined using the first-order reaction equation:

ln(Cf / Ci) = -kt

where Ci is the initial concentration, Cf is the final concentration, k is the rate constant, and t is the time.

In this case, Cf = 0.256 M, Ci is what we want to find, k = 0.039/second, and t = 145 seconds.

Rearranging the equation, we have:

ln(Cf / Ci) = -kt

ln(0.256 / Ci) = -0.039 * 145

Using logarithmic properties, we can rewrite the equation as:

ln(Ci / 0.256) = 0.039 * 145

Taking the exponential of both sides, we have:

Ci / 0.256 =
`e^(0.039 * 145)`

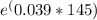
Now, solve for Ci:

Ci = 0.256 *
`e^(0.039 * 145)`

Ci ≈ 0.256 *
`e^5.655`

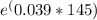
Ci ≈ 0.256 * 285.72

Ci ≈ 73.21 M

Therefore, the initial concentration of the reaction was approximately 73.21 M.

To find the half-life, we can use the equation:

t1/2 = (ln2) / k

where t1/2 is the half-life and k is the rate constant.

Plugging in the given value of k:

t1/2 = (ln2) / 0.039

t1/2 ≈ 17.72 seconds

Therefore, the half-life of the reaction is approximately 17.72 seconds.