Question

Question 4) Identify the area of the trapezoid

rounded to the nearest tenth.
18 in
3x in
5.8 in

Answer 1

Check the picture below.

`\textit{Area of a Trapezoid}\\\\ A=\cfrac{h(a+b)}{2}~~ \begin{cases} h~~=height\\ a,b=\stackrel{parallel~sides}{bases~\hfill }\\[-0.5em] \hrulefill\\ a=5.8\\ b=18\\ h=3x \end{cases}\implies A=\cfrac{3x(5.8+18)}{2} \\\\\\ A=\cfrac{3x(23.8)}{2}\implies A=3x(11.9)\implies \boxed{A=35.7x}`

Answer 2

Area = 35.7x in²

Explanation:

The formula for the area of a trapezoid is:

`\boxed{\begin{array}{l}\underline{\textsf{Area of a trapezoid}}\\\\A=(1)/(2)(a+b)h\\\\\textsf{where:}\\ \phantom{ww}\bullet\;\textsf{$A$ is the area.}\\ \phantom{ww}\bullet\;\textsf{$a$ and $b$ are the parallel sides (bases).}\\\phantom{ww}\bullet\;\textsf{$h$ is the height.}\end{array}}`

In this case:

• 
  `a = 18 \;\sf in`
• 
  `b = 5.8 \;\sf in`
• 
  `h = 3x\;\sf in`

To find the area of the trapezoid, we can substitute the given values into the formula and solve for A:

`A=(1)/(2)(18 + 5.8) \cdot 3x`

`A=(1)/(2)(23.8) \cdot 3x`

`A=11.9 \cdot 3x`

`A=35.7x\; \sf in^2`

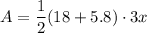
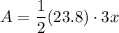
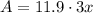
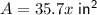
Therefore, the area of the trapezoid is 35.7x in².

Please note that as the height (h) of the trapezoid in the given diagram is 3x in, we can only find the area in terms of x. If you have been given the value of x, you can substitute this into 35.7x to find the area of the trapezoid.