The value for
 is approximately
is approximately
 .
.
The equation given is
 , where
, where
 is the pressure loss,
is the pressure loss,
 is a constant,
is a constant,
 is the flow rate, and
is the flow rate, and
 is another constant.
is another constant.
Given values:
-
 (Pa·m³/s)
(Pa·m³/s)
-
 (m³/s)
(m³/s)
-
 (Pa)
(Pa)
We can substitute these values into the equation to solve for
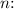
![\[ P = KQ^n \]](https://img.qammunity.org/2024/formulas/engineering/college/ocpv6k2132yxrgmaqlue1r9j2hhohuvs6q.png)
![\[ 180 = (190 * 10^3) * (0.04)^n \]](https://img.qammunity.org/2024/formulas/engineering/college/ej785rzo14sx64mcqyxut6k2qqmoup0fxx.png)
To find
 , take the natural logarithm (ln) of both sides:
, take the natural logarithm (ln) of both sides:
![\[ \ln(180) = \ln[(190 * 10^3) * (0.04)^n] \]](https://img.qammunity.org/2024/formulas/engineering/college/5vyjh8f7g9d6i9em6bdxuwy0a3k5t5dudf.png)
Now, apply logarithm properties to simplify:
![\[ \ln(180) = \ln(190 * 10^3) + n * \ln(0.04) \]](https://img.qammunity.org/2024/formulas/engineering/college/moz9bz10jjtys6xvdtbobgtkpon220dml6.png)
Now, solve for
 :
:
![\[ n = (\ln(180) - \ln(190 * 10^3))/(\ln(0.04)) \]](https://img.qammunity.org/2024/formulas/engineering/college/r6o9cxbyjkvwdhnwmhcw1fmi286zo87hx9.png)
Let's calculate this:
![\[ n = (\ln(180) - \ln(190 * 10^3))/(\ln(0.04)) \]](https://img.qammunity.org/2024/formulas/engineering/college/r6o9cxbyjkvwdhnwmhcw1fmi286zo87hx9.png)
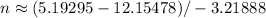
![\[ n \approx (-6.96183)/(-3.21888) \]](https://img.qammunity.org/2024/formulas/engineering/college/u4qjg0iyih6tft4mj2wvorxp834ft38hrp.png)
![\[ n \approx 2.162 \]](https://img.qammunity.org/2024/formulas/engineering/college/qiitqnl7cjajcnm3m7s9xrj486m0xx94sn.png)
So, the value for
 is approximately
is approximately
 .
.