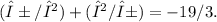Final Answer:
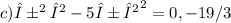
The equation with roots
 For the quadratic equation
For the quadratic equation
 with roots α and β, the value of
with roots α and β, the value of
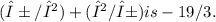
Step-by-step explanation:
The given quadratic equation is x^2 - 2x - 5 = 0. Let α and β be the roots of this equation. The product of the roots (αβ) is equal to the constant term divided by the coefficient of the quadratic term, which is -5/1 = -5. Now, we are asked to find the equation whose roots are α^2β and αβ^2. We know that if α and β are the roots of a quadratic equation, then the new equation with roots
 Therefore, the required equation is
Therefore, the required equation is
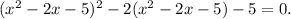
Now, let's simplify this equation:
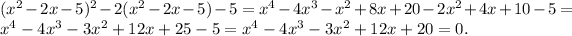
The roots of this new equation are α^2β and αβ^2. Now, for the second part of the question, we are given the quadratic equation
 . We are required to find the value of (α/β) + (β/α). Using the fact that α and β are the roots, we have
. We are required to find the value of (α/β) + (β/α). Using the fact that α and β are the roots, we have
 . Using the formulas
. Using the formulas
 we get
we get
 . Therefore, the final answer is
. Therefore, the final answer is