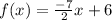 is the linear representation of the given function.
is the linear representation of the given function.
To determine whether f(x) represents a linear function, we can check if the ratio of the differences in f(x) and x is constant. If it is, then the function is linear.
Let's calculate the differences:


Now, let's calculate the ratio:
![\[\text{Ratio} = \frac{\text{Difference in } f(x)}{\text{Difference in } x} = (-7)/(2)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/nh3yqzs935amuhizplpiftglq0fmq91d6r.png)
Since the ratio is constant,
 represents a linear function. Now, let's find the equation in the form
represents a linear function. Now, let's find the equation in the form
 .
.
We know that
 , the slope, is given by the ratio. So,
, the slope, is given by the ratio. So,
![\[m = (-7)/(2)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/muhj9xslzgdljrgwrbyv6wq5e6mus48qkm.png)
Now, let's use the point-slope form of a line
 with one of the points from the table. Let's use the point
with one of the points from the table. Let's use the point
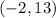 :
:
![\[f(x) - 13 = (-7)/(2)(x - (-2))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/1etezcmrs2f55kdw3462p6mtqbtwrs5sd0.png)
Simplify this equation:
![\[f(x) - 13 = (-7)/(2)(x + 2)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/8r39tzgi7aep0uwvztbhcbur7w3lj5rqfg.png)
Now, solve for
 :
:
![\[f(x) = (-7)/(2)x - 7 + 13\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/fz5763olpkktyxwkcuiqo366nckow9hvi1.png)
Combine the constants:
![\[f(x) = (-7)/(2)x + 6\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/2wmofosh45h3o7nr9q6mm1mics62kcn5wd.png)
So,
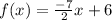 is the linear representation of the given function.
is the linear representation of the given function.