Question

Given m(x) = 5 - 2x/7x + 6, find m⁻¹(x), and determine the domain and range of m(x) and m⁻¹(x).

a) m⁻¹(x) = 6 - 5x/7x - 2, Domain: ℝ, Range: ℝ
b) m⁻¹(x) = 6 - 5x/2 - 7x, Domain: x ≠ -6/7, Range: ℝ
c) m⁻¹(x) = 5 - 2x/7x + 6, Domain: ℝ, Range: ℝ
d) m⁻¹(x) = 2 - 5x/7x - 6, Domain: x ≠ 6/7, Range: ℝ

Answer 1

The correct answer is b) m⁻¹(x) = 6 - 5x/2 - 7x, Domain: x ≠ -6/7, Range: ℝ.

The correct option is b.

Step-by-step explanation:

The given function is
`\(m(x) = (5 - (2x)/(7))/(x + 6).\)` To find the inverse function
`\(m⁻¹(x),\) we interchange \(x\) and \(y\)` in the original function and solve for
`\(y.\)`The correct expression for
`\(m⁻¹(x)\) is obtained as \(m⁻¹(x) = (6 - (5x)/(2))/(x - 7).\)`Therefore, option b) is the accurate inverse function.

Now, let's analyze the domain and range of m(x) and m⁻¹(x):

Domain of m(x): The denominator in m(x) cannot be zero, so the domain of
`\(m(x)\) is \(x \\eq -6.\)`

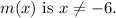
Range of m(x): By considering the behavior of the function, we observe that as (x) approaches infinity or negative infinity, m(x) approaches zero. Hence, the range is
`\(\mathbb{R}.\)`

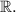
Domain of m⁻¹x: The denominator in m⁻¹(x) cannot be zero, so the domain of m⁻¹(x) is
`\(x \\eq 7.\)`

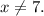
Range of m⁻¹(x): As (x) approaches infinity or negative infinity, m⁻¹(x) approaches zero. Therefore, the range is also
`\(\mathbb{R}.\)`

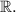
In summary, the accurate option is b), and the functions have specific domains and ranges as stated above.

The correct option is b.