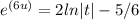Question

Solve the separable differential equation for u dudt=e6u+3t. Use the following initial condition: u(0)=−5 . u=

Answer 1

The solution to the differential equation with the given initial condition is:
`e^((6u)) = 2 ln|t| - 5/6`

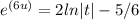
To solve the separable differential equation: u
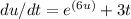`du/dt = e^((6u)) + 3t`, we can rearrange the equation as follows:

`du/(e^((6u))) = (1/3t) dt`

Now, we can integrate both sides.

On the left side, we can use the substitution v = 6u, which means dv = 6 du:

(1/6) ∫
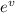`e^v`dv = (1/3) ∫ (1/t) dt

Integrating both sides, we get:

(1/6)
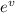`e^v` = (1/3) ln|t| + C

Now, substitute back v = 6u:

`(1/6) e^((6u)) = (1/3) ln|t| + C`

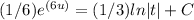
Finally, to find the particular solution, we can use the given initial condition u(0) = -5:

`(1/6) e^((6(-5))) = (1/3) ln|0| + C`

Simplifying, we find C = -5/6.

Therefore, the solution to the differential equation with the given initial condition is:

`e^((6u)) = 2 ln|t| - 5/6`