Question

I was reading a book on DFT the other day, and the author included asymptotic behavior for Eₓc [rho(r)].

Given that, do we know the asymptotic behavior for kinetic energy and/or total energy in DFT?

Answer 1

we know the asymptotic behavior for the kinetic energy
`(\(T_s[\rho]\))` and total energy
`(\(E[\rho]\))` in Density Functional Theory (DFT) is known.

Step-by-step explanation:

In the asymptotic behavior of the kinetic energy,
`\(T_s[\rho]\)`, the dependence on the electron density
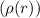`(\(\rho(r)\))` as r goes to infinity is characterized by the term
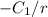`\(-C_1/r\)`. This term reflects the long-range behavior of the kinetic energy density in the presence of a finite number of electrons. The constant
`\(C_1\)` captures the system-specific details, and the negative sign signifies the decrease in kinetic energy as electrons move away.

Similarly, for the total energy,
`\(E[\rho]\)`, the asymptotic behavior is also characterized by a term that goes as
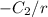`\(-C_2/r\)` as r approaches infinity. Here,
`\(C_2\)` represents another constant that encapsulates the system's characteristics. The negative sign indicates the decrease in total energy as one moves to the outer regions of the system. Understanding these asymptotic behaviors is crucial in analyzing the long-range effects in DFT calculations, providing insights into the behavior of the system at large distances.

In summary, the asymptotic behaviors of the kinetic and total energies in DFT involve terms proportional to
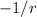`\(-1/r\)`, where constants
`\(C_1\)` and
`\(C_2\)` encapsulate the system-specific details, offering valuable information about the long-range behavior of these energy components.