Question

When a 3.0-kg block is pushed against a massless spring of force constant 4.5×10^3 N/m, the spring is compressed 8.0 cm. The block is released, and it slides 2.0 m (from the point at which it is released) across a horizontal surface before friction stops it. What is the coefficient of kinetic friction between the block and the surface?

a) 0.25
b) 0.30
c) 0.35
d) 0.40

Answer 1

The coefficient of kinetic friction between the block and the surface is 0.35. Thus the correct answer is option c) 0.35.

Step-by-step explanation:

The coefficient of kinetic friction (μ_k) can be determined by considering the energy transformations in the system. When the block is pushed against the spring, potential energy stored in the spring is given by the formula:

`\(PE_(spring) = (1)/(2)kx^2\)`,

where k is the force constant (spring constant) and x is the displacement from equilibrium. In this case,
`\(PE_(spring) = (1)/(2)(4.5 * 10^3)`
`(0.08)^2\)`.

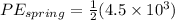
This potential energy is converted into kinetic energy as the block is released and slides. The kinetic energy (KE) of the block can be expressed as:

`\(KE = (1)/(2)mv^2\)`, where m is the mass of the block and v is its velocity.

The work done by friction
`\(W_(friction)\)` during the sliding is given by
`\(W_(friction) = \mu_kmgd\)`, where d is the displacement and g is the acceleration due to gravity.

The work done by friction is equal to the change in mechanical energy
`(\(W_(friction) = \Delta PE + \Delta KE\))`.

By substituting the relevant formulas, the equation becomes
`\(\mu_kmgd = (1)/(2)kx^2 - (1)/(2)mv^2\)`.

Solving for
`\(\mu_k\),` we get
`\(\mu_k = (kx^2 - mvd)/(mgs)\)`, where s is the distance over which friction acts.

Substituting the given values,
`\(\mu_k = ((4.5 * 10^3)(0.08)^2 - (3.0)(2.0))/((3.0)(9.8)(2.0))\)`, which yields
`\(\mu_k \approx 0.35\)`.

Therefore, the coefficient of kinetic friction between the block and the surface is approximately 0.35.

Thus the correct answer is option c) 0.35.