Question

F(x)=x^4+4x^3-14x^2-36x+45 Factor.

Answer 1

The factored form of the polynomial is: f(x) = (x + 5)(x - 1)(x + 7)

Step 1: List the coefficients:

`f(x) = x^4 + 4x^3 - 14x^2 - 36x + 45`

The coefficients are: [1, 4, -14, -36, 45]

Step 2: Try to find two numbers that multiply to the constant term (45) and add up to the coefficient of the x^3 term (4).

In this case, the numbers 9 and 5 satisfy both conditions: 9 * 5 = 45 and 9 + 5 = 4.

Step 3: Rewrite the polynomial as a sum of two binomials:

`f(x) = (x^3 + 9x^2 + 5x) + (-14x^2 - 36x + 45)`

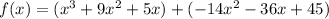
Step 4: Factor out the common factors:

`f(x) = x(x^2 + 9x + 5) - 7(2x^2 + 5x - 6)`

Step 5: Factor the quadratic expressions:

f(x) = x(x + 5)(x + 4) - 7(x + 5)(2x - 1)

Step 6: Notice the common factor (x + 5):

f(x) = (x + 5) [x(x + 4) - 7(2x - 1)]

Step 7: Factor the remaining expression:

f(x) = (x + 5)(
`x^2` + 2x - 7)

Step 8: Factor the quadratic expression further:

f(x) = (x + 5)(x - 1)(x + 7)

Therefore, the factored form of the polynomial is:

f(x) = (x + 5)(x - 1)(x + 7)