Main Answer:
The potential function for
 is given by the option:
is given by the option:
c)
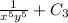
Step-by-step explanation:
The potential function
 for a given function
for a given function
 is found by integrating each term with respect to its corresponding variable. In this case, if
is found by integrating each term with respect to its corresponding variable. In this case, if
 , the potential function
, the potential function
 is obtained by integrating with respect to
is obtained by integrating with respect to
 and
and
 separately.
separately.
![\[ F(x, y) = \int (1)/(x^5 y^5) \,dx = -(1)/(4x^4 y^5) + g(y) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/drbohvy4lzr2b0pbynzj7vnwolxxvh16w3.png)
Now, we integrate
 with respect to
with respect to
 :
:
![\[ F(x, y) = \int -(1)/(4x^4 y^5) \,dy = (1)/(x^5 y^4) + C \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/p5ow5r55nfy5pmnl6eihd4x427iyo3cflg.png)
So, the correct option is c)
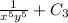 , where
, where
 is the constant of integration.
is the constant of integration.