when you multiply a less negative number by a positive number that is getting smaller, the product will become less negative. This means
 is becoming less negative as
is becoming less negative as
 increases, or in other words,
increases, or in other words,
 is increasing.
is increasing.
Therefore, the correct statement is:
C.
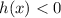 and is strictly increasing.
and is strictly increasing.
The given function
 is a product of two functions,
is a product of two functions,
 and
and
 .
.
Here is what we know about these functions:
-
 is strictly increasing and
is strictly increasing and
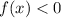 for all values of
for all values of
 .
.
-
 is strictly decreasing and
is strictly decreasing and
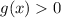 for all values of
for all values of
 .
.
Now, let's analyze the product
 :
:
- Since
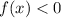 and
and
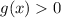 , their product
, their product
 will be negative for all
will be negative for all
 . This means
. This means
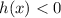 .
.
- For the nature of
 in terms of increasing or decreasing:
in terms of increasing or decreasing:
- When \( x \) increases,
 increases because
increases because
 is strictly increasing.
is strictly increasing.
- At the same time,
 decreases because
decreases because
 is strictly decreasing.
is strictly decreasing.
- The rate of increase of
 and the rate of decrease of \( g(x) \) will determine the nature of
and the rate of decrease of \( g(x) \) will determine the nature of
 .
.
- However, without specific information about the rates of change of
 and
and
 , we cannot definitively say whether
, we cannot definitively say whether
 is increasing or decreasing.
is increasing or decreasing.
Here's what we can infer:
- Since
 is negative and increasing, it is getting closer to zero from the negative side as
is negative and increasing, it is getting closer to zero from the negative side as
 increases, which makes
increases, which makes
 less negative.
less negative.
- Since
 is positive and decreasing, it is getting closer to zero as
is positive and decreasing, it is getting closer to zero as
 increases, but remains positive.
increases, but remains positive.
Now, when you multiply a less negative number by a positive number that is getting smaller, the product will become less negative. This means
 is becoming less negative as
is becoming less negative as
 increases, or in other words,
increases, or in other words,
 is increasing.
is increasing.
Therefore, the correct statement is:
C.
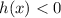 and is strictly increasing.
and is strictly increasing.
the complete Question is given below: