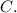answer:
To find the degree of an angle given two sides of a triangle, you can use the law of cosines. The formula is:
![\[ c^2 = a^2 + b^2 - 2ab \cdot \cos(C) \]](https://img.qammunity.org/2024/formulas/mathematics/college/4se7oprcvqt1ju5rfri1cvxsvqjgytuuvf.png)
Where
 and
and
 are the lengths of the sides of the triangle and
are the lengths of the sides of the triangle and
 is the angle opposite side \(c\).
is the angle opposite side \(c\).
Let's denote the sides as follows:
 (one side)
(one side)
 (another side)
(another side)
 would be the side opposite to the angle we're trying to find.
would be the side opposite to the angle we're trying to find.
To find the angle
 , we rearrange the law of cosines formula:
, we rearrange the law of cosines formula:
![\[ \cos(C) = (a^2 + b^2 - c^2)/(2ab) \]](https://img.qammunity.org/2024/formulas/mathematics/college/1jrmdofx8m22zov8dgw56349hlia2ip6g2.png)
In this case, we're looking to find angle
 opposite to the side of length 14 and 5. Substituting the given values:
opposite to the side of length 14 and 5. Substituting the given values:
![\[ \cos(C) = (14^2 + 5^2 - c^2)/(2 * 14 * 5) \]](https://img.qammunity.org/2024/formulas/mathematics/college/l8al0rkjt2wb5uzdzd5uezb5oednfwwpt9.png)
![\[ \cos(C) = (196 + 25 - c^2)/(140) \]](https://img.qammunity.org/2024/formulas/mathematics/college/5yo9m9ctbm87cspyg8tf9xlt6kuo02rmla.png)
\
![[ \cos(C) = (221 - c^2)/(140) \]](https://img.qammunity.org/2024/formulas/mathematics/college/f5gjqqy98hsspx3fz9exj9x6faogornmts.png)
Now, let's solve for
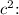
![\[ 221 - c^2 = 140 \cdot \cos(C) \]](https://img.qammunity.org/2024/formulas/mathematics/college/y9fyl1qglc3xrpi7ztegh9fcy6v7rlgqq1.png)
![\[ c^2 = 221 - 140 \cdot \cos(C) \]](https://img.qammunity.org/2024/formulas/mathematics/college/x510v7nakij2e5njdf2msv9qae1y3v5b1p.png)
![\[ c^2 = 221 - 140 \cdot \cos(C) \]](https://img.qammunity.org/2024/formulas/mathematics/college/x510v7nakij2e5njdf2msv9qae1y3v5b1p.png)
To find the degree of angle
 take the inverse cosine (arccos) of the value obtained for
take the inverse cosine (arccos) of the value obtained for
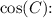
![\[ C = \arccos\left((221 - c^2)/(140)\right) \]](https://img.qammunity.org/2024/formulas/mathematics/college/6dv8ujbnywka56vjfw8bxck98jjr7agz2i.png)
Please note that to compute the exact degree of angle
 we need to know the exact length of the third side
we need to know the exact length of the third side
 or have further information about the triangle. If you have the value of the side
or have further information about the triangle. If you have the value of the side
 you can substitute it into the equation to find the degree of angle
you can substitute it into the equation to find the degree of angle