Question

Determine the area of the region bounded by y=4x³ and y=100x

Answer 1

By definite integrals, the area of the region is equal to 625 square units.

How to determine the area between the two curves

In this problem we must determine the area between two curves by definite integrals. First, determine the points of intersection of the two curves:

4 · x³ = 100 · x

4 · x³ - 100 · x = 0

4 · x · (x² - 25) = 0

4 · x · (x + 5) · (x - 5) = 0

x = 0 or x = - 5 or x = 5

y = 100 · 0

y = 0

y = 100 · (- 5)

y = - 500

y = 100 · 5

y = 500

Third, determine the area between the two curves: (f(x) = 100 · x, g(x) = 4 · x³)

`I = \int\limits^0_(-5) {[g(x) - f(x)]} \, dx + \int\limits^5_0 {[f(x) - g(x)]} \, dx`

`I = \int\limits^0_(- 5) {[4\cdot x^3-100\cdot x]} \, dx + \int\limits^5_0 {[100\cdot x - 4\cdot x^3]} \, dx`

`I = x^4|_(-5)^(0) - 50 \cdot x^2|_(-5)^(0) + 50 \cdot x^2|_(0)^(5)-x^(4)|_(0)^(5)`

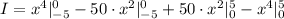
I = 0⁴ - (- 5)⁴ - 50 · 0² + 50 · (- 5)² + 50 · 5² - 50 · 0² - 5⁴ + 0⁴

I = 0 - 625 + 0 + 1250 + 1250 - 0 - 625 + 0

I = 625 + 625

I = 1250