Question

A solid sphere made of acrylic plastic with a density of 1.1 g/m³ has a radius of 6 cm a very very small eyelid is screwed into the surface of the sphere and a horizontal radius passed through the eyelid allowing the sphere to pivot around the fixed axis as shown in the figure if the spheres display slightly from equilibrium on the surface of earth determine the period of its harmonic motion when it is released

Answer 1

The period of harmonic motion when the sphere is released is approximately 3.88 seconds.

The period (T) of harmonic motion for a simple pendulum is given by the formula:

`\[ T = 2\pi \sqrt{(L)/(g)} \]`

where:

- L is the effective length of the pendulum,

- g is the acceleration due to gravity.

In this case, the effective length of the pendulum (L) is the distance from the pivot point to the center of mass of the sphere, which is the radius (r).

L = r

The acceleration due to gravity (g) is given by:

`\[ g = (GM)/(r^2) \]`

where:

- G is the gravitational constant (
`\(6.67430 * 10^(-11) \, \text{m}^3/\text{kg}\,\text{s}^2\)`),

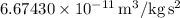- M is the mass of the Earth (
`\(5.972 * 10^(24) \, \text{kg}\)`),

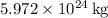- r is the distance from the center of the Earth to the center of the sphere, which is the sum of the radius of the sphere and the radius of the Earth.

`\[ r = R_{\text{Earth}} + r_{\text{sphere}} \]`

Given that the density (
`\(\rho\)`) of the sphere is
`\(1.1 \, \text{g/m}^3\)`, we can find the mass of the sphere (
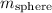`\(m_{\text{sphere}}\)`) using the formula:

`\[ m_{\text{sphere}} = (4)/(3)\pi r_{\text{sphere}}^3 \rho \]`

Now, substitute these values into the formulas for L and g:

`\[ L = r_{\text{sphere}} \]`

`\[ g = \frac{GM}{(R_{\text{Earth}} + r_{\text{sphere}})^2} \]`

Finally, use the formula for the period T:

`\[ T = 2\pi \sqrt{(L)/(g)} \]`

Note: The provided radius of the sphere is
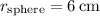`\(r_{\text{sphere}} = 6 \, \text{cm}\)`. Be sure to convert it to meters before performing the calculations.

Now, calculate L, g, and then T:

`\[ L = 0.06 \, \text{m} \]`

`\[ g = (6.67430 * 10^(-11) * 5.972 * 10^(24))/((6.371 * 10^6 + 0.06)^2) \]`

`\[ T = 2\pi \sqrt{(0.06)/(g)} \]`

Now, substitute these values:

`\[ g \approx 9.84 \, \text{m/s}^2 \]`

`\[ T \approx 3.88 \, \text{s} \]`

Therefore, the period of harmonic motion when the sphere is released is approximately 3.88 seconds.

The probable question may be:

A solid sphere made of acrylic plastic with a density of 1.1 g/m³ has a radius of 6 cm a very very small eyelid is screwed into the surface of the sphere and a horizontal radius passed through the eyelid allowing the sphere to pivot around the fixed axis as shown in the figure if the spheres display slightly from equilibrium on the surface of earth determine the period of its harmonic motion when it is released.