Question

Prove the following statement using a direct proof: If a is an odd integer, then a² - a + 1 is an odd integer.

Answer 1

If a is an odd integer, then a² - a + 1 is an odd integer ,this statement is true. Starting with the assumption that a is an odd integer (a = 2k + 1), substituting it into a² - a + 1 yields 4k² + 2k + 1. As all terms except the constant 1 are divisible by 2, the expression conforms to the definition of an odd integer (2m + 1), proving the initial statement.

Step-by-step explanation:

Let
`\( a \)` be an odd integer, which means it can be expressed as a = 2k + 1, where k is an integer. Now, substitute this expression for
`a` into a² - a + 1 :

`a^2 - a + 1 &= (2k + 1)^2 - (2k + 1) + 1 \\`

`&= 4k^2 + 4k + 1 - 2k - 1 + 1 \\`

`&= 4k^2 + 2k + 1.`

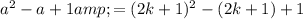
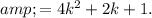
This expression can be written as
`\( 2(2k^2 + k) + 1 \)`, where
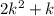`\( 2k^2 + k \)` is an integer. Therefore,
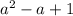`\( a^2 - a + 1 \)` is of the form 2n + 1, where n is an integer. By definition, any integer of the form 2n + 1 is odd. Hence,
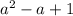`\( a^2 - a + 1 \)` is an odd integer when a is an odd integer.

In conclusion, starting with the assumption that
`\( a \)` is an odd integer, we demonstrated that
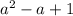`\( a^2 - a + 1 \)` can be expressed in the form 2n + 1, proving that it is indeed an odd integer. This completes the direct proof of the given statement.