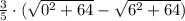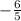Evaluate the following integral using U-substitution. \int\limits^0_6 {\frac{3x}{5\sqrt{x^(2)+64} } \, dx

Question

Evaluate the following integral using U-substitution.


`\int\limits^0_6 {\frac{3x}{5\sqrt{x^(2)+64} } \, dx`

Answer 1

The result of the integral by algebraic substitution is equal to
`-(6)/(5)`.

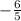How to solve an integral by algebraic substitution

Herein we find the case of an integral that can be solved by algebraic substitution, whose procedure is shown below:

1. Create a substitution formula and its derivative.
2. Apply the previous expressions on the integral.
3. Use derivative rules to find the solution.
4. Revert substitution formula.
5. Use the definition of definite integral.

Step 1: Create a substitution formula and its derivative:

u = x² + 64, du = 2 · x dx

Step 2: Apply the previous expression on the integral:

`(3)/(10) \int\limits^0_6 {(2\cdot x)/(√(x^2+64)) } \, dx`

`(3)/(10) \int\limits^(u(0))_(u(6)) {\frac{du}{u^{(1)/(2) }} }`

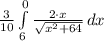
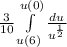
Step 3: Use derivative rules to find the solution:

`(3)/(5)\cdot u^{(1)/(2)}|_(u(6))^(u(0))`

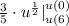
Step 4: Revert substitution formula:

`(3)/(5)\cdot √(x^2+64)|_(6)^(0)`

Step 5: Use the definition of definite integral:

`(3)/(5)\cdot (√(0^2+64) - √(6^2+ 64))`

`-(6)/(5)`