The length of AC = 5.102 units. .
How to solve
Using the theorem of similar right triangles, we have
Recall, that the theorem of similar right triangles states that if an angle in one right triangle is equal to an angle in another, and their hypotenuses are proportional, they're similar.
DC/AC = BC/AC
Cross multiply
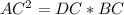
Substitute the given values

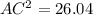
We expand using the square.
AC =
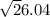
Therefore, it can be seen that the length of AC = 5.1 units.