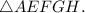Question

4. Is AABCD similar to AEFGH?

A
33.5 ft
27 ft
18 ft
D
H
16.5 ft 11 ft
90° 90°
B 21 ft C
E
23 ft
90° 90°
G 14 ft F

Answer 1

No,
`\( \triangle AABCD \)` is not similar to
`\( \triangle AEFGH \)`as their corresponding side ratios
`(\(AB:AE, BC:EF, CD:FG\))` are not equal, despite both triangles having right angles.

To determine if
`\( \triangle AABCD \)` is similar to
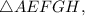`\( \triangle AEFGH \),` we need to check if their corresponding angles are congruent and if their corresponding sides are in proportion.

Given the information provided:

1. Angles
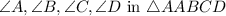`\( \angle A, \angle B, \angle C, \angle D \) in \( \triangle AABCD \)`are all right angles (90° each).

2.
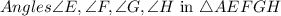`Angles \( \angle E, \angle F, \angle G, \angle H \) in \( \triangle AEFGH \)` are all right angles (90° each).

Since both triangles have corresponding right angles, we can focus on the side lengths:

`\(AB = 33.5 \, \text{ft}, BC = 27 \, \text{ft}, CD = 18 \, \text{ft}\) in \( \triangle AABCD \).`

`\(AE = 23 \, \text{ft}, EF = 14 \, \text{ft}, FG = 16.5 \, \text{ft}\) in \( \triangle AEFGH \).`

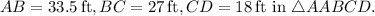
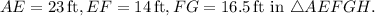
To check for similarity, we need the ratios of corresponding sides to be equal. Let's calculate the ratios:

`\[(AB)/(AE) = (33.5)/(23) \approx 1.457\]`

`\[(BC)/(EF) = (27)/(14) \approx 1.929\]`

`\[(CD)/(FG) = (18)/(16.5) \approx 1.091\]`

The ratios are not equal, so
`\( \triangle AABCD \)` is not similar to
`\( \triangle AEFGH \).`