Question

A 0.50 kg mass is attached to a string 1.0 meter long and moves in a horizontal circle at a rate of 0.5 seconds per revolution.Calculate the tension in the string.

Answer 1

The tension in the string is calculated using centripetal force. For a mass of 0.50 kg attached to a string with a length of 1.0 meter moving at 12.56 m/s, the tension is found to be 78.75 N.

Step-by-step explanation:

Calculating the Tension in the String

To calculate the tension in the string, we need to recognize that the tension provides the centripetal force necessary to keep the mass moving in a circle. Given that a 0.50 kg mass is attached to a 1.0 meter long string and completes a revolution every 0.5 seconds, we can use the formula for centripetal force,
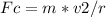`Fc = m*v2/r`, where m is the mass, v is the velocity, and r is the radius of the circle. First, we calculate the velocity by finding the circumference of the circle
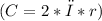`(C = 2*π*r)`and dividing it by the time for one revolution (T). The circumference here is
`2*π*1.0 m = 6.28 m`, and with T = 0.5 s, the velocity becomes 6.28 m / 0.5 s = 12.56 m/s. The centripetal force is thus
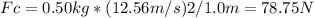`Fc = 0.50 kg * (12.56 m/s)2 / 1.0 m = 78.75 N`, which is the tension in the string.