Question

Classify ABC by its side and by its angle’s

Answer 1

Triangle ABC, with vertices A(-2,0), B(6,2), and C(-1,4), is classified as a scalene triangle. All three sides (AB, BC, AC) and all three angles (
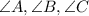`\( \angle A, \angle B, \angle C \)`) are different.

To classify triangle ABC based on its sides and angles, we can use the distance formula to find the lengths of the sides and the slope formula to determine the angles.

Coordinates of Points:

- A(-2, 0)

- B(6, 2)

- C(-1, 4)

Side Lengths:

1.
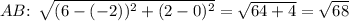
`\( AB \): \( √((6 - (-2))^2 + (2 - 0)^2) = √(64 + 4) = √(68) \)`

2.
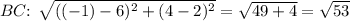
`\( BC \): \( √(((-1) - 6)^2 + (4 - 2)^2) = √(49 + 4) = √(53) \)`

3.
`\( AC \): \( √(((-1) - (-2))^2 + (4 - 0)^2) = √(1 + 16) = √(17) \)`

Angle Measures:

1.
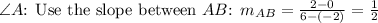
`\( \angle A \): Use the slope between \( AB \): \( m_(AB) = (2 - 0)/(6 - (-2)) = (1)/(2) \)`

2.
`\( \angle B \): Use the slope between \( BC \): \( m_(BC) = (4 - 2)/((-1) - 6) = -(1)/(7) \)`

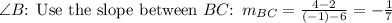
3.
`\( \angle C \): Use the slope between \( AC \): \( m_(AC) = (4 - 0)/((-1) - (-2)) = 4 \)`

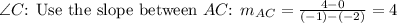
Classification:

- By Sides:

-
`\( \triangle ABC \)` is a scalene triangle since all side lengths (AB, BC, AC) are different.

- By Angles:

-
`\( \triangle ABC \)` is a scalene triangle since all angle measures (
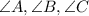`\( \angle A, \angle B, \angle C \)`) are different.

So,
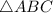`\( \triangle ABC \)` is a scalene triangle based on both sides and angles.