Question

Trigonometric Form of a Complex Number: Write the complex number z=-2i in trigonometric form.

Answer 1

The trigonometric form of the complex number
`\(z = -2i\) is \(z = 2 \angle -(\pi)/(2)\).`

Step-by-step explanation:

To express the complex number
`\(z = -2i\)` in trigonometric form, we utilize the polar form
`\(z = r \angle \theta\),` where
`\(r\)` denotes the magnitude of the complex number, and
`\(\theta\)` represents the argument. First, calculating the magnitude
`(\(r\)),` we take the absolute value of
`\(z\)` , yielding
`\(| -2i | = 2\).`

This magnitude,
`\(r = 2\)` , serves as the radial distance from the origin to the complex number in the complex plane. Next, determining the argument
`(\(\theta\)),` we consider the angle formed by the complex number. For
`\(z = -2i\),` the argument is
`\(-(\pi)/(2)\)` since the number lies along the negative imaginary axis.

Substituting these values back into the polar form, we arrive at
`\(z = 2 \angle -(\pi)/(2)\)` . In this representation, the magnitude
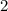`\(2\)` signifies the distance from the origin, and
`\(-(\pi)/(2)\)` denotes the angle with respect to the positive real axis. Thus, the trigonometric form succinctly conveys the complex number's geometric properties in the polar coordinate system, providing both magnitude and direction information. In summary,
`\(z = 2 \angle -(\pi)/(2)\)` serves as a concise and precise representation of the complex number
`\(z = -2i\)` in trigonometric form.

Answer 2

The complex number z = -2i in trigonometric form is
`\(z = 2 \text{cis}\left((3\pi)/(2)\)\)`, where 2 is the magnitude and
`\((3\pi)/(2)\)` is the argument.

Step-by-step explanation:

To express the complex number z = -2i in trigonometric form, we use the polar form of a complex number, which is given by
`\(z = r \text{cis}(\theta)\)`, where r is the magnitude and
`\(\theta\)` is the argument.

In this case, the magnitude r is the absolute value of the complex number, which is the distance of the point from the origin in the complex plane. For z = -2i, the magnitude r is 2.

The argument
`\(\theta\)` is the angle formed by the complex number in the polar coordinate system. The complex number z = -2i lies along the negative imaginary axis, which corresponds to an angle of
`\((3\pi)/(2)\)` radians in standard position. Therefore, z = -2i can be expressed in trigonometric form as z = 2
`\text{cis}\left((3\pi)/(2)\)\).`