Question

You deposit $5,000 in an account that pays 2.25% interest compounded quarterly. Round your answer to the nearest dollar. What will be the total amount in the account after 2 years?

Answer 1

After 2 years, the total amount in the account will be approximately $5,229.

Step-by-step explanation:

Compounded interest calculations involve the use of the formula A =
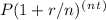`P(1 + r/n)^(^n^t^)` , where:

- A is the future value of the investment/loan, including interest.

- P is the principal amount (initial deposit).

- r is the annual interest rate (in decimal form).

- n is the number of times that interest is compounded per year.

- t is the time the money is invested or borrowed for in years.

In this scenario, the principal (P) is $5,000, the annual interest rate (r) is 2.25%, the interest is compounded quarterly (n = 4), and the investment period is 2 years (t = 2). Plugging these values into the formula, we get:

`\[A = 5000 \left(1 + (0.0225)/(4)\right)^((4 * 2))\]`

Solving this equation gives us the future value of the investment after 2 years, which is approximately $5,229. This means that with an initial deposit of $5,000 and a 2.25% interest rate compounded quarterly, the account will grow to around $5,229 after 2 years.

Compounded interest is powerful because it allows you to earn interest not just on your initial deposit but also on the interest that accumulates over time. In this case, the quarterly compounding contributes to the overall growth of the investment, resulting in a slightly higher total amount compared to simple interest calculations.