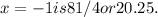Question

Let f(x)=9 e⁻ˣ / 4.
f⁴(-1)=

Answer 1

`x = -1 is 81/4 or 20.25.`

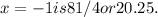
The fourth iterate of the function
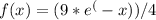`f(x) = (9 * e^(-x))/4`, evaluated at

`x = -1`, yields the result 81/4 or 20.25.

Step-by-step explanation:

The notation f⁴(-1) represents the fourth iterate of the function f(x) evaluated at x = -1. To calculate this, we need to repeatedly apply the function four times. Let's break down the calculations step by step.

The function
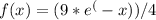`f(x) = (9 * e^(-x))/4` is given. To find
`f⁴(-1)`, we first find
`f²(x)`by applying the function twice:

`\[f²(x) = f(f(x)) = (9)/(4)e^{-\left((9)/(4)e^(-x)\right)}.\]`

Now, applying this function once more to get f³(x):

\[f²(x) = f(f(x)) = \frac{9}{4}e^{-\left(\frac{9}{4}e^{-x}\right)}.\]
`\[f²(x) = f(f(x)) = (9)/(4)e^{-\left((9)/(4)e^(-x)\right)}.\]`

Finally, applying the function for the fourth time to get f⁴(x):

`\[f⁴(x) = f(f³(x)) = (9)/(4)e^{-\left((9)/(4)e^{-\left((9)/(4)e^{-\left((9)/(4)e^(-x)\right)}\right)}\right)}.\]`

Now, substituting x = -1 into this expression, we get
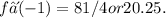`f⁴(-1) = 81/4 or 20.25.`Therefore, the fourth iterate of the given function evaluated at

`x = -1 is 81/4 or 20.25.`