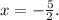Final Answer
Therefore the answer is
![\[ x = -(5)/(2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/sdwlljgaha0wn1yzo4jso3v9g48zgn3uon.png)
Step-by-step explanation
The given equation is
 To solve this equation, we'll first find a common denominator. The denominators in this case are
To solve this equation, we'll first find a common denominator. The denominators in this case are
 The common denominator is
The common denominator is
 Now, multiply each term by the missing factors to clear the fractions.
Now, multiply each term by the missing factors to clear the fractions.
![\[ x(x+2)(x+2) + 3x(x+5) = 2(x+5)(x+2) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/7s1roz1xpjwo0zlfmin5a0y05f3lmywywc.png)
Next, simplify and combine like terms:
![\[ x(x^2+4x+4) + 3x^2 + 15x = 2(x^2+7x+10) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/bo4pvqm08z3jf7kh0qjzisjcrtl2nj4jkm.png)
Expand and collect like terms:
![\[ x^3 + 4x^2 + 4x + 3x^2 + 15x = 2x^2 + 14x + 20 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/yesrb6n23l7qh1lkacwofrofoo8ozj3oro.png)
Combine like terms again:
![\[ x^3 + 7x^2 + 19x - 2x^2 - 14x - 20 = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ofu5imuhgism8wl0pexr31tcjkqt4sqadp.png)
Finally, simplify the equation:
![\[ x^3 + 5x^2 + 5x - 20 = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/wyjqc845y0opfu0xrbnie3vjn8zk1784r0.png)
Now, factor the cubic equation or use numerical methods to find the solutions. The solution is
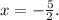
Therefore, the final answer to the given equation is