Question

A new centrifugal pump is being considered for an application involving the pumping of ammonia. The specification is that the flow rate be more than 5 gallons per minute (gpm). In an initial study, eight runs were made. The average flow rate was 6.5 gpm and the standard deviation was 1.9 gpm. If the mean flow rate is found to meet the specification, the pump will be put into service. What is the P-value

Answer 1

from the t-distribution table, at df = 7 and t = 2.23

Lies p-values [ 0.05 and 0.025 ]

Hence;

0.025 < p-value < 0.05

Explanation:

Given that;

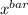`x^(bar)` = 6.5 gpm

μ = 5 gpm

n = eight runs = 8

standard deviation σ = 1.9 gpm

Test statistics;

t = (
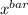`x^(bar)` - μ) /
`(s)/(√(n) )`

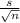
we substitute

t = (6.5 - 5) /
`(1.9)/(√(8) )`

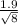
t = 1.5 / 0.67175

t = 2.23

the degree of freedom df = n-1 = 8 - 1

df = 7

Now, from the t-distribution table, at df = 7 and t = 2.23

Lies p-values [ 0.05 and 0.025 ]

Hence;

0.025 < p-value < 0.05