The function g(x) has the lowest minimum at (-1, -2), f(x) has a minimum at (0, 0), and h(x) has the highest minimum at (-3, 4). The transformations applied to the parent function f(x) =
 determine the minimum points of g(x) and h(x).
determine the minimum points of g(x) and h(x).
The relationship between the minimums of the functions f(x) =
 , g(x) =
, g(x) =
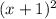 – 2, and h(x) =
– 2, and h(x) =
 + 4 involves understanding the transformations of parent functions. The function f(x) is a standard parabola with its vertex at the origin (0, 0), which is also its minimum point. The function g(x) has been horizontally shifted one unit to the left and vertically shifted two units down, thus the vertex of g(x) is at (-1, -2), meaning its minimum is lower than f(x)'s. Similarly, h(x) is horizontally shifted three units to the left and vertically shifted four units up, making its vertex at (-3, 4), so its minimum is higher than both f(x) and g(x).
+ 4 involves understanding the transformations of parent functions. The function f(x) is a standard parabola with its vertex at the origin (0, 0), which is also its minimum point. The function g(x) has been horizontally shifted one unit to the left and vertically shifted two units down, thus the vertex of g(x) is at (-1, -2), meaning its minimum is lower than f(x)'s. Similarly, h(x) is horizontally shifted three units to the left and vertically shifted four units up, making its vertex at (-3, 4), so its minimum is higher than both f(x) and g(x).
Comparing the minimum points, we find that g(x) has the lowest minimum, followed by f(x), and then h(x) has the highest minimum among the three functions.