Question

Determine if the triangles are similar. Justify your response by showing your work and circle one of the four choices below. Circle one:

a) AA
b) SAS
c) SSS
d) Not Similar
10
12
15
12

Answer 1

The triangles are similar based on the Side-Side-Side c) (SSS) criterion, as the corresponding sides are in proportion.

Step-by-step explanation:

The given triangles can be determined as similar using the Side-Side-Side (SSS) similarity criterion. In the given set of triangles, the corresponding sides are proportional. Let's denote the corresponding sides of the triangles as
`\(a_1, b_1, c_1\)` and
`\(a_2, b_2, c_2\)`respectively, where
`\(a\)` is the side opposite the angle
`\(A\), \(b\)` is the side opposite the angle
`\(B\)`, and
`\(c\)` is the side opposite the angle
`\(C\)`.

Now, comparing the corresponding sides:

1.
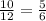
`\((10)/(12) = (5)/(6)\)`

2.
`\((12)/(15) = (4)/(5)\)`

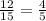
3.
`\((15)/(12) = (5)/(4)\)`

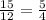
Since all corresponding sides are in proportion, we can conclude that the triangles are similar by the SSS criterion.

In mathematical terms:

`\[ (a_1)/(a_2) = (10)/(12) = (5)/(6), \quad (b_1)/(b_2) = (12)/(15) = (4)/(5), \quad (c_1)/(c_2) = (15)/(12) = (5)/(4) \]`

The ratios are consistent, confirming the similarity of the triangles. Therefore, the correct choice is c) SSS, indicating that the triangles are similar based on the Side-Side-Side criterion.