Question

the width of a rectangle is 28 centimeters. the perimeter can be no more than 380. Write and solve an inequality to find the possible lengths of the rectangle.

Answer 1

`\sf Inequality: 2 * (L + 28) \leq 380`

`\sf L \leq 162`

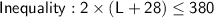
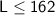
Explanation:

Let's denote the length of the rectangle as
`\sf L`. The perimeter (
`\sf P`) of a rectangle is given by the formula:

`\sf P = 2 * (\text{length} + \text{width})`

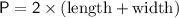
In this case, the width (
`\sf \text{width}`) is given as 28 centimeters, and the perimeter should be no more than 380 centimeters.

So, the inequality representing the perimeter constraint is:

`\sf 2 * (L + 28) \leq 380`

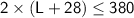
Now, let's solve for
`\sf L`:

`\sf 2L + 56 \leq 380`

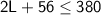
Subtract 56 from both sides:

`\sf 2L + 56 -56 \leq 380 -56`

`\sf 2L \leq 324`

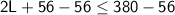
Divide by 2 on both sides:

`\sf (2L )/(2) \leq (324)/(2)`

`\sf L \leq 162`

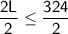
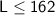
So, the possible lengths of the rectangle (
`\sf L`) should be less than or equal to 162 centimeters to ensure that the perimeter is no more than 380 centimeters