Question

Now consider the second-order, linear differential equation (1−t)y′′ +ty′ −y=(1−t)² . Carry out each of the following steps to find the complete solution y (t) of the differential equation: a. Guess (it's quite easy) a non-zero solution y₁ of its null equation. b. Use the method of reduction of order to find a second solution y₂ of the null equation that is linearly independent of y₁ . c. Compute W(y₁ ,y₂). d. Find a particular solution yₚ (t) of the complete equation. e. Put together the information that you have gathered above to write y (t).

Answer 1

The complete solution
`\(y(t)\)` of the second-order linear differential equation
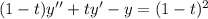`\((1-t)y'' + ty' - y = (1-t)^2\)` is given by
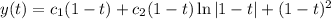`\(y(t) = c_1(1-t) + c_2(1-t) \ln|1-t| + (1-t)^2\)`, where
`\(c_1\)` and
`\(c_2\)` are arbitrary constants.

Step-by-step explanation:

To find the complete solution, we first guess a non-zero solution
`\(y_1\)` of the null equation, which is the homogeneous part of the differential equation. A suitable guess is
`\(y_1 = 1-t\)`. Then, using the reduction of order method, we find a second solution \(y_2\) that is linearly independent of
`\(y_1\)`. The general form of
`\(y_2\)` is
`\(y_2 = y_1 \int (1)/(y_1^2)e^{-\int (t)/(1-t) dt} dt\).` After obtaining
`\(y_1\)` and
`\(y_2\)`, we compute the Wronskian
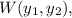`\(W(y_1, y_2)\),` which is given by
`\(W(y_1, y_2) = y_1y_2' - y_1'y_2\).`

Next, we find a particular solution
`\(y_p\)` of the complete equation using the method of undetermined coefficients or variation of parameters. In this case, a particular solution can be
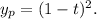`\(y_p = (1-t)^2\).` Finally, combining the homogeneous and particular solutions, we write the general solution
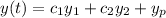`\(y(t) = c_1y_1 + c_2y_2 + y_p\)`, where
`\(c_1\)` and
`\(c_2\)` are constants determined by initial conditions.

The reason for this solution lies in the linearity of the differential equation. The general solution is a linear combination of the homogeneous solutions
`\(y_1\)` and
`\(y_2\)`, and the particular solution
`\(y_p\)`. The constants
`\(c_1\) and \(c_2\)` are determined by the initial conditions, providing a unique solution for a given set of conditions.