Question

You may use your book, notes, and handouts but, do not get any help from anyone else! Do not go online, do not work with anyone else. Show work that justifies your answer to receive full credit. Put f

Answer 1

The derivative of f(x) is
`f'(x) = cos(1/x) - (sin(1/x) * (1/x^2)) * x.`

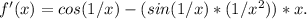
Step-by-step explanation:

To find the derivative of the function
`f(x) = xcos(1/x)`, we can use the product rule.

The product rule states that if we have a function
`h(x) = g(x) * j(x)`, then
`h'(x) = g'(x) * j(x) + g(x) * j'(x)`.

Here, g(x) = x and j(x) = cos(1/x). Taking the derivatives of g(x) and j(x), we get
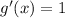`g'(x) = 1` and
`j'(x) = -sin(1/x) * (1/x^2`).

Using the product rule, we have
`f'(x) = g'(x) * j(x) + g(x) * j'(x) = 1 * cos(1/x) + x * (-sin(1/x) * (1/x^2)).`

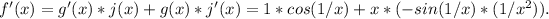
So, the derivative of f(x) is
`f'(x) = cos(1/x) - (sin(1/x) * (1/x^2)) * x`.

Your question is incomplete, but most probably the full question was:

You may use your book, notes, and handouts but, do not get any help from anyone else! Do not go online, do not work with anyone else. Show work that justifies your answer to receive full credit. Put final answer in the blank. Use pencil only. Papers done in ink or illegible papers will not be graded.

If
`f(x)=xcos(1/x)`

find f′(x).