Question

Each of the regions A, B, and C bounded by the graph of f and the x-axis has area 3. Find the value of

2
[f(x) + 2x + 6] dx.

−4

Answer 1

The value of the given integral is 3.

To find the value of the integral
`\int\limits^2_(-4) [f(x)+2x+6]dx`, we can use the given information that each of the regions A, B, and C bounded by the graph of f and the x-axis has an area of 3.

Let's denote the area of each region as follows:

Area(A)=
`\int\limits^b_a f(x)dx`

Area(B)=
`\int\limits^a_b f(x)dx`

Area(C)=
`\int\limits^d_c f(x)dx`

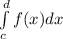
Since each of these areas is 3, we can write the following equations:

Area(A)=
`\int\limits^b_a f(x)dx=3`

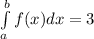
Area(B)=
`\int\limits^a_b f(x)dx=3`

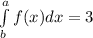
Area(C)=
`\int\limits^d_c f(x)dx=3`

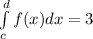
Now, let's express the given integral in terms of these areas:

`\int\limits^2_(-4) [f(x)+2x+6]dx=` ​
`\int\limits^b_a [f(x)+2x+6]dx +`
`\int\limits^c_b [f(x)+2x+6]dx +`
`\int\limits^d_c [f(x)+2x+6]dx`

Now, substitute the values of the areas:

​
`\int\limits^2_(-4) [f(x)+2x+6]`

`\int\limits^2_(-4) [f(x)dx = -A+B-C= -3 +3-3 = -3\\\\-3+6 =3`

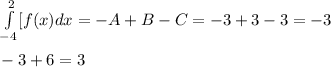
So, the value of the given integral is 3.

Question